Heap이라는 자료구조에 대해

Heap이라는 자료구조에 대해

• heap 정의
• 힙을 배열로 구현
• 삽입과 삭제로 깨진 힙을 재구조화하기(heapify)
• 참고 출처

heap 정의

힙 자료구조는 완전 이진 트리를 기초로 하는 자료구조입니다. 완전 이진트리는 마지막을 제외한 모든 노드에서 자식들이 꽉 채워진 이진트리를 말합니다.

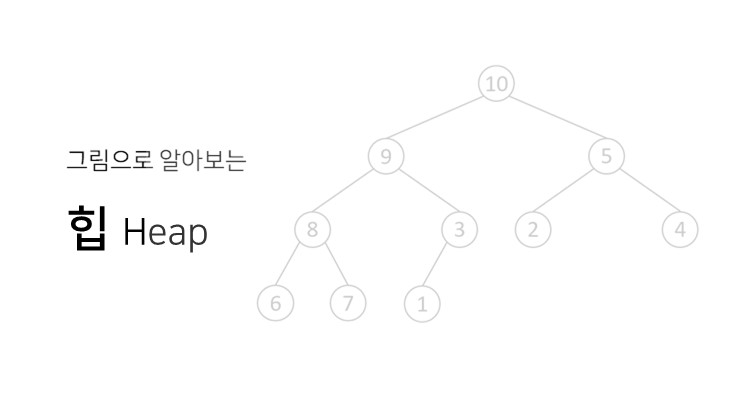
다음과 같은 특징들을 가짐

1. 힙은 최대힙(Max heap)과 최소힙(Min Heap)으로 나눠집니다. 최대힙은 부모노드의 값이 자식노드들의 값보다 항상 크고, 최소힙은 부모노드의 값이 자식노드의 값보다 항상 작습니다. (위 그림은 최대힙의 예시) 이러한 성질 때문에 항상 느슨한 정렬상태(반정렬 상태)를 유지합니다.
2. 힙은 중복값을 허용합니다. 힙은 최댓값 또는 최솟값을 쉽게 뽑기 위한 자료구조 임으로 중복을 허용합니다.

힙을 배열로 구현

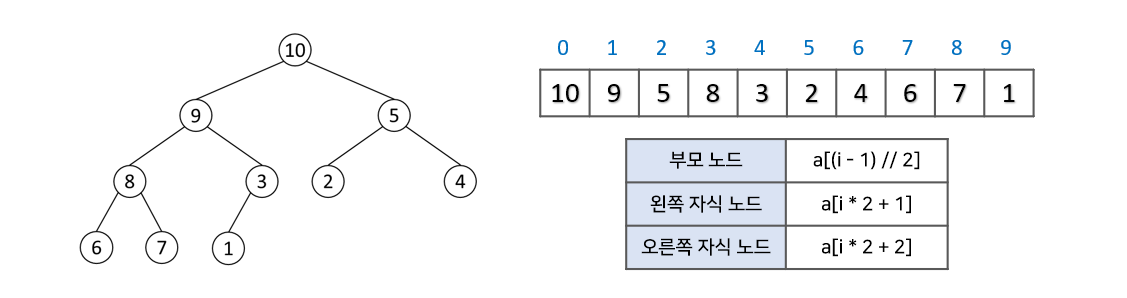
힙은 대체적으로 배열로 구현됩니다. 완전이진트리를 기본으로 하기 때문에 비었는 공간이 없어 배열로 구현하기에 용이합니다.

아래 그림과 같이 루트노드를 배열의 0번 index에 저장하고, 각 노드를 기점으로 왼쪽 자식노드는 a[i∗2+1], 오른쪽 자식노드는 a[i∗2+2] 의 index에 저장됩니다. 또한 특정 index의 노드에서 부모노드는 a[(i−1)//2]로 찾을 수 있습니다.

삽입과 삭제로 깨진 힙을 재구조화하기(heapify)

최대힙의 부모노드는 항상 자식노드의 값보다 크다는 조건을 가지고 있습니다. 하지만 힙에서 삽입 또는 삭제가 일어나게 되면 경우에 따라 최대힙의 조건이 깨질 수 있습니다. 이러한 경우에 최대힙의 조건을 만족할 수 있게 노드들의 위치를 바꿔가며 힙을 재구조화(heapify) 해주어야 합니다.

삽입과 삭제의 경우 모두 연산 자체는 O(1)로 작동하지만 heapify의 과정을 거치기 때문에 O(logn)의 시간복잡도를 가지게 됩니다.

삽입 과정

먼저 삽입과정입니다. 아래 그림은 새로운 노드가 삽입되었을 경우입니다. 새로운 노드는 리프노드가 아니면서 가장 말단에 있는 노드의 자식 노드로 추가됩니다. 이후, 부모노드와 비교하면서 재구조화 과정을 수행합니다. 삽입과정은 아래에서 위로 재구조화 과정이 이루어지게 됩니다.

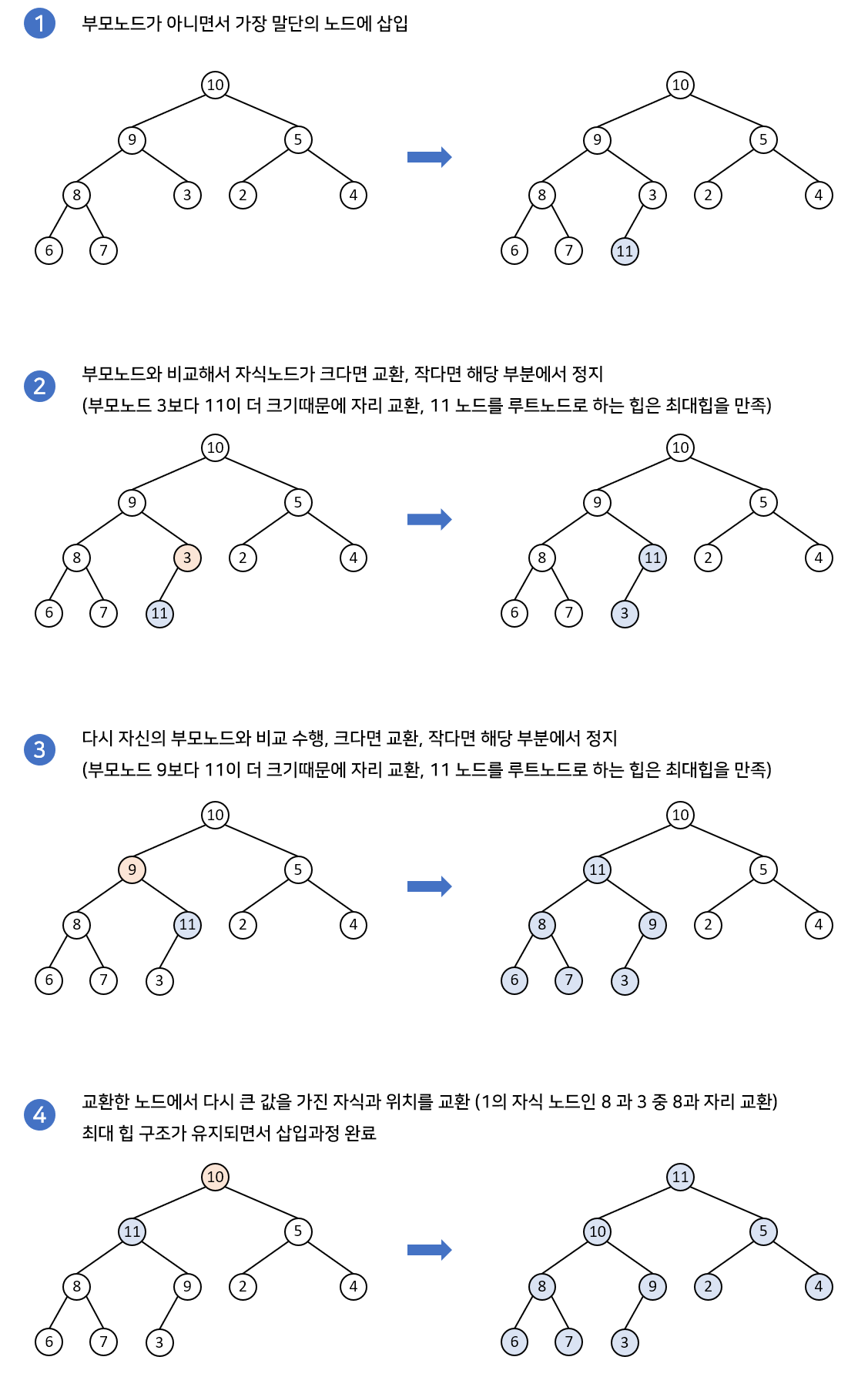
삽입 코드 구현

def up_heapify(index, heap):
    child_index = index
    while child_index != 0:
        parent_index = (child_index - 1) // 2
        if heap[parent_index] < heap[child_index]:
            heap[parent_index], heap[child_index] = heap[child_index], heap[parent_index]
            child_index = parent_index
        else:
            return

삭제 과정

아래 그림은 루트 노드가 삭제되었을 경우입니다. 루트노드가 삭제되면 가장 말단노드를 루트노드자리에 대체한 후 재구조화 과정을 수행합니다. 힙으로 구현된 우선순위 큐에서도 가장 우선순위가 큰 루트노드를 주로 삭제합니다. 삽입의 경우에는 가장 말단노드에 추가하여 재구조화 과정을 수행하면 됩니다. 삭제과정은 위에서 아래로 재구조화 과정이 이루어지게 됩니다.

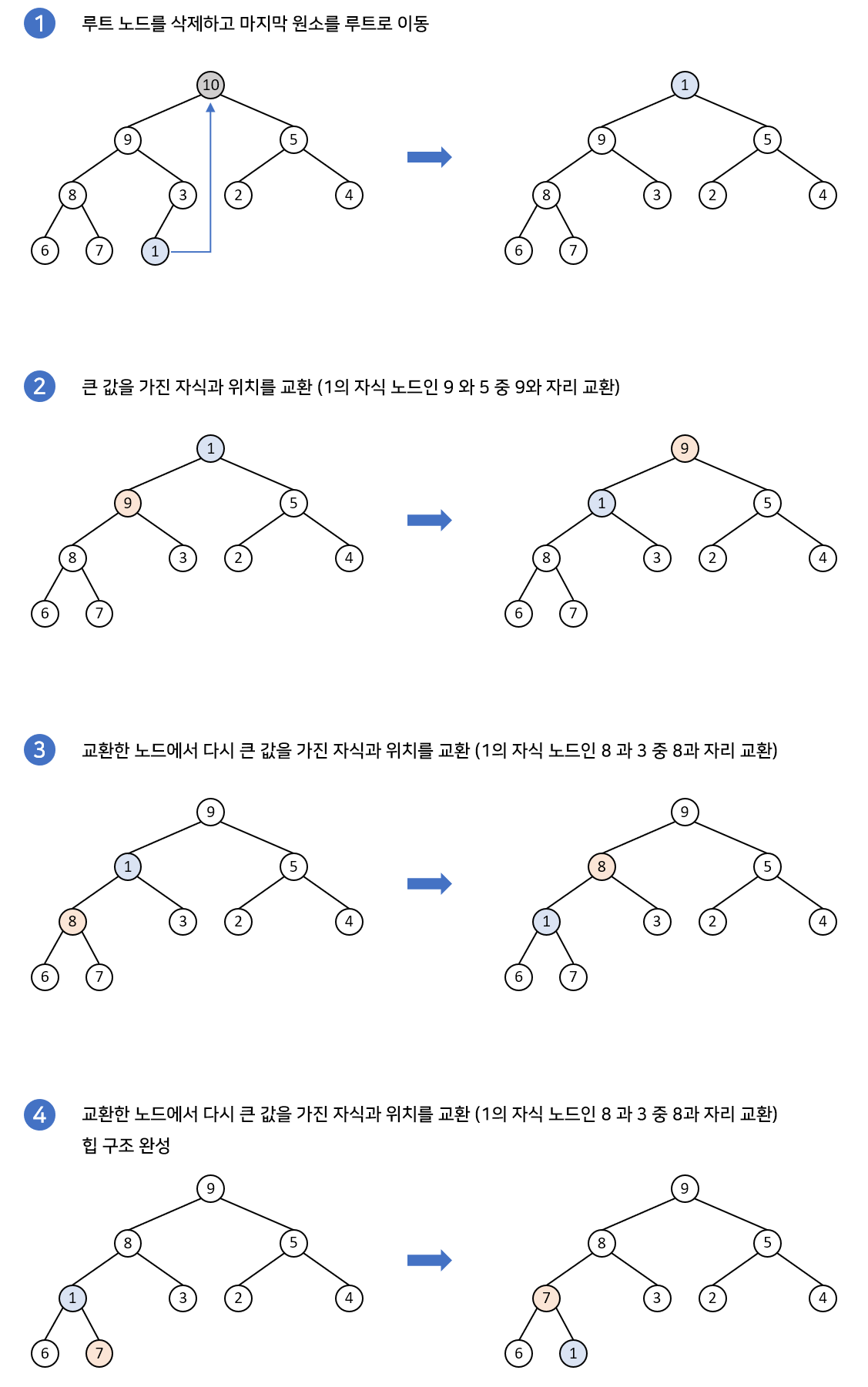
삭제 코드 구현

def find_bigger_child_index(index, heap_size):
    parent = index
    left_child = (parent * 2) + 1
    right_child = (parent * 2) + 2

    if left_child < heap_size and heap[parent] < heap[left_child]:
        parent = left_child
    if right_child < heap_size and heap[parent] < heap[right_child]:
        parent = right_child
    return parent


def down_heapify(index, heap):
    parent_index = index
    bigger_child_index = find_bigger_child_index(parent_index, len(heap))
    while parent_index != bigger_child_index:
        heap[parent_index], heap[bigger_child_index] = heap[bigger_child_index], heap[parent_index]
        parent_index = bigger_child_index
        bigger_child_index = find_bigger_child_index(parent_index, len(heap))

재귀함수를 사용하면 다음과 같습니다.

def down_heapify(array, index, heap_size):
        
        # 1. 부모노드와 자식노드들의 인덱스 지정
        parent = index
        left_child = 2 * parent + 1
        right_child = 2 * parent + 2
		
        # 2. 왼쪽 자식노드, 오른쪽 자식노드 중 가장 큰 노드를 선택
        if left_child < heap_size and array[left_child] > array[parent]:
            parent = left_child
        if right_child < heap_size and array[right_child] > array[parent]:
            parent = right_child
            
        # 3. 자식노드 중 가장 큰 노드와 부모 노드를 바꿈(배열의 값 교환)
        if parent != index:
            array[parent], array[index] = array[index], array[parent]
            
            # 4. 바뀐 자식노드의 힙을 재구조화
            make_heap(array, parent, heap_size)

힙이 아닌 배열을 힙으로 만들기(build heap)

heapify의 경우 기본적으로 힙을 만족하는 경우에서 삽입 또는 삭제가 발생할 때 O(logn)의 시간복잡도로 다시 힙으로 만드는 과정입니다. build heap은 이와 다르게 아예 힙의 조건을 만족하지 않는 배열을 힙으로 만드는 과정입니다. 여러번의 heapify 과정을 거치기 때문에 결과적으로 시간복잡도는 O(nlogn)입니다.

재귀함수를 이용한 재구조

재귀함수 과정으로 아랫방향 재구조를 실행할 수 있습니다.아래 과정에서는 해당 재구조 방법을 사용하겠습니다.

재구조 과정

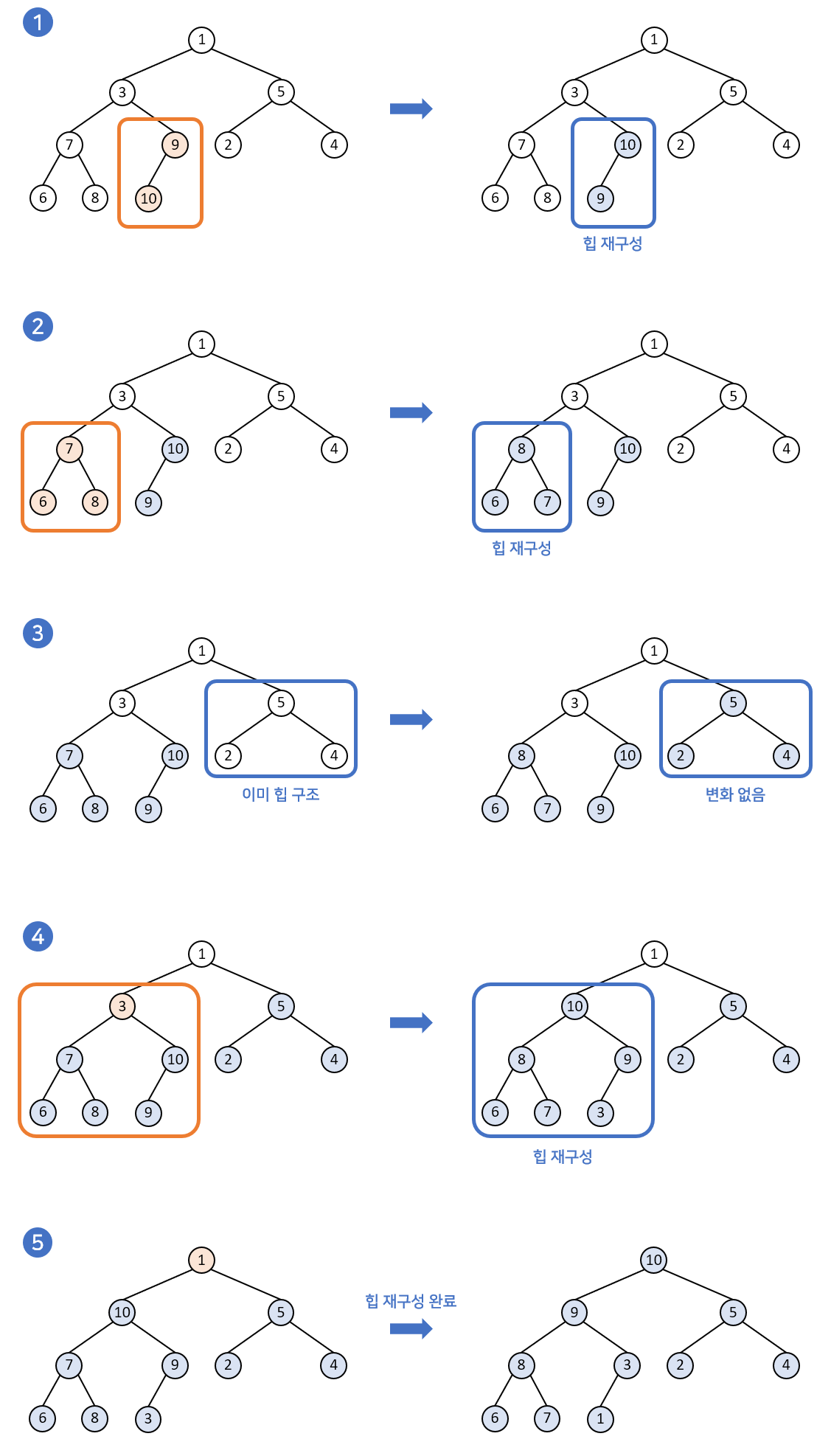
build heap의 과정은 가장 말단의 부모-자식 노드에서부터 시작합니다. 부모노드가 될 수 있는 노드들만을 골라서 진행한다고 생각하면 편할 것 같습니다. 가장 뒤에서부터 heapify가 진행되기 때문에 그림의 4번과정 같은 경우를 보면 모든 자식트리들은 이미 힙의 구조를 만들고 있어 heapify가 가능해집니다.

재구조 코드 구현

재귀함수로 구현하면 다음과 같습니다. 위 down heapify 과정을 부모노드가 될 수 있는 노드만을 골라 뒤에서부터 실행해주면 됩니다.

def make_heap(array, index, heap_size):
        parent = index
        left_child = 2 * parent + 1
        right_child = 2 * parent + 2

        if left_child < heap_size and array[left_child] > array[parent]:
            parent = left_child
        if right_child < heap_size and array[right_child] > array[parent]:
            parent = right_child
        if parent != index:
            array[parent], array[index] = array[index], array[parent]
            make_heap(array, parent, heap_size)
	
    # 부모노드가 되는 노드들만을 골라서 뒤에서부터 heapify를 차례로 실행
    for i in range((N - 1) // 2, -1, -1):
        make_heap(array, i, heap_size)

참고 출처

https://velog.io/@emplam27/자료구조-그림으로-알아보는-힙Heap